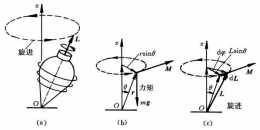
陀螺的進動，重力力矩使角動量方向改變產生進動，那如果我在陀螺的質心位置再施加一個沿重力的力會怎麼樣？

作者：由邱笑陽發表于舞蹈時間：2019-09-20

先放一下結論：對於一個正在做規則進動的陀螺，如果在其質心處施加一個豎直向下的恆力，那麼在一階精度下，

陀螺會做週期性的章動，其進動角速度和自轉角速度也會呈現出週期性變化；

這種週期性變化的振幅與施加的力的大小成正比，而週期與陀螺原本的自轉角速度成反比。

對一些基本的物理量進行定義：陀螺的質量為

，質心到固定點的距離為

，初始時刻與豎直線之間的夾角為

$\theta_0$

，重力加速度大小為

，陀螺的三個轉動慣量為

（假設陀螺繞自轉軸旋轉對稱），其中

是陀螺繞自轉軸的轉動慣量，在陀螺質心處施加的向下的力為

。

為了避免概念混淆，我們說一下陀螺運動的三個部分：

進動：陀螺繞著豎直線的轉動，體現為陀螺在地面上的投影做順時針或逆時針轉動。對應的進動角為

$\psi$

，進動角速度為

$\dot{\psi}$

；

章動：陀螺與豎直線之間的夾角變化，體現為陀螺在地面上的投影長度變長或變短。對應的章動角為

$\theta$

，章動角速度為

$\dot\theta$

；

自轉：這個應該最好理解，像地球那樣繞著自轉軸轉動。對應的自轉角為

$\varphi$

，自轉角速度為

$\dot\varphi$

。

然後建立座標系。為了方便起見，我們如下圖所示建立一個隨著陀螺一起做進動和章動的座標系

，這樣的好處是

軸始終垂直於陀螺自轉軸且始終保持水平，

軸始終與陀螺自轉軸貼合。

設陀螺的角速度在這一座標系下的各個分量為

$\bm\omega=(\omega_1,\omega_2,\omega_3)$

，

那麼陀螺的動量矩為

$\mathbf J\bm\omega=(J_1\omega_1,J_1\omega_2,J_3\omega_3)$

，

重力和外力

的合力矩

$\begin{aligned} \mathbf M&=(0,0,a)\times((mg+F)\sin\theta,0,-(mg+F)\cos\theta)\\ &=(0,(mg+F)a\sin\theta,0) \end{aligned}$

陀螺的進動角速度

$\dot{\bm\psi}=(-\dot\psi\sin\theta,0,\dot\psi\cos\theta)$

章動角速度

$\dot{\bm\theta}=(0,\dot\theta,0)$

自轉角速度

$\dot{\bm\varphi}=(0,0,\dot\varphi)$

所以，隨陀螺做進動和章動的座標系

的角速度

$\bm\Omega=\dot{\bm\psi}+\dot{\bm\theta}=(-\dot\psi\sin\theta,\dot\theta,\dot\psi\cos\theta)$

因為陀螺的運動能被分解成進動、章動、自轉三部分，所以有

$\bm\omega=\dot{\bm\psi}+\dot{\bm\theta}+\dot{\bm\varphi}$

，即

$\left\{ \begin{aligned} \omega_1&=-\dot\psi\sin\theta\\ \omega_2&=\dot\theta\\ \omega_3&=\dot\psi\cos\theta+\dot\varphi \end{aligned} \right.\tag{1}$

也可以從（1）式中反解出

$\dot\psi,\dot\theta,\dot\varphi$

$\left\{ \begin{aligned} \dot\psi&=-\frac{\omega_1}{\sin\theta}\\ \dot\theta&=\omega_2\\ \dot\varphi&=\omega_1\cot\theta+\omega_3 \end{aligned} \right.\tag{2}$

完成了上述準備工作，我們可以列出陀螺的動力學方程

$\mathbf J\frac{d\bm\omega}{dt}+\bm\Omega\times(\mathbf J\bm\omega)=\mathbf{M}$

，即

$\left\{ \begin{aligned} &J_1\frac{d\omega_1}{dt}-J_3\dot\theta\omega_3-J_1\dot\psi\omega_2\cos\theta=0\\ &J_1\frac{d\omega_2}{dt}+J_3\dot\psi\omega_3\sin\theta-J_1\dot\psi\omega\cos\theta=(mg+F)a\sin\theta\\ &J_3\frac{d\omega_3}{dt}-J_1\dot\psi\omega_2\sin\theta+J_1\dot\theta\omega_1=0 \end{aligned} \right.\tag{3}$

之後，對（3）式進行一些簡化，可以解出其一階精度下的解（相關假設以及解法放在回答的最後）

$\left\{ \begin{aligned} \omega_1&=-\dot\psi_0\sin\theta_0+\frac{Fa\sin\theta_0}{J_3\dot\varphi_0}[1-\cos(\frac{J_3}{J_1}\dot\varphi_0 t)]\\ \omega_2&=\frac{Fa\sin\theta_0}{J_3\dot\varphi_0}\sin(\frac{J_3}{J_1}\dot\varphi_0 t)\\ \omega_3&=\dot\varphi_0+\dot\psi_0\cos\theta_0 \end{aligned} \right.$

再透過（2）式，我們可以得到陀螺進動、章動、自轉的情況（同樣是精確至一階精度）

$\left\{ \begin{aligned} \dot\psi&=\dot\psi_0-\frac{Fa}{J_3\dot\varphi_0}[1-\cos(\frac{J_3}{J_1}\dot\varphi_0t)]\\ \dot\theta&=\frac{Fa\sin\theta_0}{J_3\dot\varphi_0}\sin(\frac{J_3}{J_1}\dot\varphi_0t)\\ \dot\varphi&=\dot\varphi_0+\frac{Fa\cos\theta_0}{J_3\dot\varphi_0}[1-\cos(\frac{J_3}{J_1}\dot\varphi_0t)] \end{aligned} \right.$

其中

$\dot\psi_0,\dot\varphi_0$

分別是陀螺做規則進動時的進動角速度和自轉角速度。

所以，對於一個正在做規則進動的陀螺，如果在質心處施加一個力

，那麼陀螺運動情況是：

對於進動部分，進動角速度

$\dot\psi$

呈餘弦變化，且

$\dot\psi\leq\dot\psi_0$

。這說明，進動角速度會因為力

的出現而減慢；

對於章動部分，可以再做一次積分，得到章動角

$\theta=\theta_0+\frac{J_1Fa\sin\theta_0}{J_3^2\dot\varphi_0^2}[1-\cos(\frac{J_3}{J_1}\dot\varphi_0t)]\leq\theta_0$

。這說明，章動角會因為力

的出現而增大，或者說陀螺的傾斜程度會增大。

對於自轉部分，自轉角速度也會出現週期性變化，且

$\dot\varphi\geq\dot\varphi_0$

。這說明，自轉角速度會因為力

的出現而加快。但由於高速轉子的自轉角速度一般都很大，所以在實際物理過程中，這種週期性的變化表現得並不明顯。

力的大小影響週期性變化的振幅，週期性變化的快慢由初始時刻的自轉角速度確定。

光看錶達式可能不太直觀，我們可以根據上面的計算結果，畫出一個做週期性進動章動的陀螺。（黑色線段代表陀螺，灰色線段是陀螺在水平面上的投影，藍色曲線是陀螺末端的軌跡，橙色虛線是豎直線）

最後我們詳細解一下陀螺的動力學方程（3）。為了把方程統一表達為關於

$\omega_1,\omega_2,\omega_3,\theta$

的表示式，我們將（2）式代入（3）式，整理得到

$\left\{ \begin{aligned} \frac{d\omega_1}{dt}&=-\frac{J_3}{J_1}\omega_2\omega_3-\omega_1\omega_2\cot\theta\\ \frac{d\omega_2}{dt}&=-\omega_1^2\cot\theta+\frac{J_3}{J_1}\omega_1\omega_3+\frac{1}{J_1}(mg+F)a\sin\theta\\ \frac{d\omega_3}{dt}&=0 \end{aligned} \right.\tag{4}$

接著，我們對方程（4）進行一定的簡化。對於規則進動的陀螺轉子，我們一般認為其自轉角速度遠大於進動角速度，即

$\dot\varphi\gg\dot\psi$

。延續這一思路，我們可以把角速度分量

$\omega_1,\omega_2$

及其導數視為一階小量（即認為陀螺進動和章動的幅度、速度、加速度等比較小），把方程（4）進一步化簡為（保留至一階量）

$\left\{ \begin{aligned} \frac{d\omega_1}{dt}&=-\frac{J_3}{J_1}\omega_2\omega_3\\ \frac{d\omega_2}{dt}&=\frac{J_3}{J_1}\omega_1\omega_3+\frac{1}{J_1}(mg+F)a\sin\theta\\ \frac{d\omega_3}{dt}&=0 \end{aligned} \right.\tag{5}$