Metamaterials and Plamonics - VOL(I).Chp(I)

作者：由慕澤發表于攝影時間：2022-01-12

VOLUME 1。 ELECTROMAGNETIC METAMATERIALS

Chapter 1。

Electromagnetic Metamaterials: Homogenization and Effective Properties of Mixtures

ARI SIHVOLA

摘要：

本章介紹了超材料和電介質混合物的均質化原理（homogenization principles）。重點在於均質化引入的新的理論：在宏觀等效表達中出現的定性的新特性，在構成材料的微觀組成成分中並不存在（

more is different

）。

經典的麥克斯韋·加奈特（Maxwell Garnett）混合結果被拿來與特性已知的複合球（composite sphere）散射問題進行比較，同時，我們將已知的混合結果轉換為簡單散射體的散射與吸收特性，這一過程中充分利用了二者之間的等價性，反之也是一樣的。

重點在於，材料的混合可以導致複合材料呈現一種意想不到的色散（dispersion）特性，這一點無法從複合材料組分的色散特性中推斷出來。

之後，等離激元奈米粒子（plasmonic nanoparticles）的局域共振特性（localized resonances）及其與幾何引數以及結構引數的關係被加以分析。

我們還討論了混合物有效介電常數（effective permittivity）的理論邊界（theoretical bounds），以及在何種情況下這些邊界值可以允許增強極化（enhanced polarization）和滲濾效應（percolation effects）。

最後，我們對各向異性特別是雙曲媒質（hyperbolic media）的徑向各向異性（radially anisotropic，RA）粒子進行了特殊的模擬，這些粒子可能顯示出出乎意料的宏觀效應，例如反常吸收（anomalous absorption）。

CONTENT

1。1。 Introduction： Electromagnetic metamaterials

（引言：電磁超材料）

1。2。 Homogenization and mixing laws

（均質化與混合法則）

1。3。 Homogenization is not dispersion-neutral

（均質化也要考慮色散）

1。4。 Homogenization is not simple arithmetic

（均質化不是簡單的加加減減）

1。5。 Conclusions： Metamaterials as Vessels of Emergence

（總結：超材料昭示著未來）

1。1。 Introduction： Electromagnetic metamaterials

超材料領域的研究日新月異。其在維基百科上的確切定義在過去的十五年（

譯註：本書出版於 2017 年

）中被修改了很多次［1-3］。無論如何，超材料研究的重點在於其新奇的材料性質，這些性質來源於構成它們的“普通材料（ordinary-material）”之間的複雜相互作用（complex interaction）。目前對超材料的定義［4］特別強調有序的材料結構，基本的材料單元將根據這些結構組合成一個超材料整體。

超材料領域的研究涵蓋了電子和微波工程（electrical and microwave engineering），光學和光子學（optics and photonics），微電子學（microelectronics），材料科學（materials science）和奈米技術（nanotechnology）等一大批學科。對該領域的關注拓展出了聲學（acoustic）、力學（mechanical）、彈性（elastic）以及熱學（elastic）的超材料等新興研究。

研究超材料的目的或者初衷之一，在於隨心所欲地控制材料屬性：材料應該是可重構的（reconfigurable），甚至是可程式設計的（programmable）。

超材料的研究溯源於電磁學（electromagnetics）。事實上，對複雜電磁材料效應（complex electromagnetic material effects）、人工材料（artificial materials）、週期結構（periodic structures）和雙各向異性（bianisotropics）的研究已經有很長的歷史，有著豐富的文獻資料［9］。

在本章中，我們將討論混合規則（mixing rules）和均質化原理（homogenization principles）在分析超材料宏觀特性中的作用。正如一句俗語所言：一道菜的最終味道並不僅僅取決於它的原料。（The taste of the final dish cannot be reduced to thoseof its ingredients。）

More Is Different。

——Philip W。 Anderson

yang元祐：【譯文】More Is Different（Philip W。 Anderson）

1.2. Homogenization and mixing laws

均質化是以一個等效引數（如等效介電常數

$\varepsilon_{\rm{}eff}$

）來表徵複合材料的性質。等效引數的適用條件是材料的異質（heterogeneities）尺寸比電磁激勵（electromagnetic excitation）的波長（wavelength）要小得多。

1.2.1. Maxwell Garnett formula and effective polarizability

一個均勻的（homogeneous）、各向同性的（isotropic）、介電常數為

$\varepsilon$

的電介質球，其在均勻靜電場中會在周圍產生偶極攝動（dipolar perturbation）。衡量這個偶極場強度的重要引數即是極化率（polarizability）。對於上述介質球，其歸一化極化率為

$\alpha = 3\dfrac{\varepsilon - 1}{\varepsilon + 2} \tag{1.1}$

接下來考慮一個稍複雜的情況，一個兩層的介質球，其外徑為

，外層介電常數為

$\varepsilon_1$

，內徑為

，內層介電常數為

$\varepsilon_2$

，此介質球的歸一化極化率為

$\alpha_{\rm{k}} = 3\dfrac{(\varepsilon_1 - 1)(\varepsilon_2 + 2\varepsilon_1) + g(2\varepsilon_1 + 1)(\varepsilon_2 - \varepsilon_1)}{(\varepsilon_1 +2 )(\varepsilon_2 + 2\varepsilon_1) + 2g(\varepsilon_1 - 1)(\varepsilon_2 - \varepsilon_1)} \tag{1.2}$

其中

$g = (a/b)^{3}$

，即內層與整個球的體積比。這一情形的幾何影象如圖 1。1 所示。

圖1。1 左圖為兩層球，右圖為均勻的等效介質球

讓我們忘記雙層球的內部結構，只考慮在均勻場激勵下與其極化率相等的一個等價均質球（這一均質化方式也稱內部均質化，internal homogenization ［12］）。這樣一個等價球的有效介電常數為

$\varepsilon_{\rm{eff}} = 1 + \dfrac{\alpha_{\rm{k}}}{1 - \alpha_{\rm{k}}/3} \tag{1.3}$

代入式（1。2），可得

$\varepsilon_{\rm{eff}} = \varepsilon_1 + 3 \varepsilon_1 g\dfrac{\varepsilon_2 - \varepsilon_1}{\varepsilon_2 + 2\varepsilon_1 - g (\varepsilon_2 - \varepsilon_1)} \tag{1.4}$

式（1。2）與經典的麥克斯韋-加奈特（MG）混合規則結論一致，該理論發表於 1904 年［14］。這一規則描述的是介電常數為

$\varepsilon_{\rm{e}}$

的背景媒質中摻雜著介電常數為

$\varepsilon_{\rm{i}}$

的物質，所佔體積比例為

，如此只要作如下等效

$\varepsilon_1 = \varepsilon_{\rm{e}}, \quad \varepsilon_2 = \varepsilon_{\rm{i}}, \quad g = p \tag{1.5}$

即可由 MG 理論出發得到有效介電常數。後文中我們將盡可能利用這一結論。

圖 1。2

1.2.2. Bruggeman mixing formula

另一個與 MG 理論共存的有效介電常數理論是布呂熱曼形式（Bruggeman formalism），公式為［15］

$(1-p)\dfrac{\varepsilon_{\rm{e}} - \varepsilon_{\rm{eff}}}{\varepsilon_{\rm{e}} + 2\varepsilon_{\rm{eff}}} + p \dfrac{\varepsilon_{\rm{i}} - \varepsilon_{\rm{eff}}}{\varepsilon_{\rm{i}} + 2\varepsilon_{\rm{eff}}} = 0 \tag{1.6}$

該式沒有給出有效引數

$\varepsilon_{\rm{eff}}$

的顯示錶達，不過這一形式的一個重點在於背景媒質

$\varepsilon_{\rm{e}}$

與內容媒質

$\varepsilon_{\rm{i}}$

是可以互換的，即作變換後

$\varepsilon_{\rm{i}} \leftrightarrow \varepsilon_{\rm{eff}}, \quad p \leftrightarrow 1-p$

後，公式仍然成立。

另一個試圖涵蓋各種均質化法則的公式是

$\dfrac{\varepsilon_{\rm{eff}} - \varepsilon_{\rm{e}}}{\varepsilon_{\rm{eff}} + 2\varepsilon_{\rm{e}} + \nu (\varepsilon_{\rm{eff}} - \varepsilon_{\rm{e}} )} = p \dfrac{\varepsilon_{\rm{i}} - \varepsilon_{\rm{e}}}{\varepsilon_{\rm{i}} + 2\varepsilon_{\rm{e}} + \nu(\varepsilon_{\rm{eff}} - \varepsilon_{\rm{e}})} \tag{1.7}$

$\nu=0$

對應 MG 理論，

$\nu = 2$

對應 Bruggeman 理論，

$\nu = 3$

對應的是其他一種理論，即所謂的

相干勢近似

（coherent potential approximation）。

1.3. Homogenization is not dispersion-neutral

多種物質複合對材料的時間色散（temporal dispersion）特性有很大影響。不管材料基本單元的色散特性如何，複合材料有效介電常數模型對應的色散性質都會非常複雜。

1.3.1. Redshifting plasmonic peaks

色散效應是等離激元超材料（plasmonic metamaterial）領域中重要的研究物件。尤其是利用極化率和混合規則的概念，可以很好地研究奈米粒子（nanoparticles）中的局域等離激元（localized plasmons）。

1。3。1。1。 Multipole resonances

式（1。1）的極化公式在

$\varepsilon = -2$

處有一奇點（singularity），此處粒子會發生“諧振（resonance）”，介質損耗（losses）非常小。

等離激元（plasmons）是很好的輻射源。測量散射的常用物理量是散射效率（scattering efficiency）

$Q_{\rm{sca}}$

，數值上等於散射截面（scattering cross-section）除以粒子的幾何截面（geometrical cross-section）［18］。對應的還有吸收（absorption）效率

$Q_{\rm{abs}}$

和消散（extinction）效率

$Q_{\rm{ext}}$

，消散量等於散射量加吸收量。對於各向同性、均勻的球體，其截面可以由洛倫茲-米（Lorenz–Mie）係數出發用球貝塞爾和漢開爾函式（spherical Bessel and Hankel functions）求得［19，20］。

圖 1。3

對於一個無損耗散射體，吸收截面應當等於 0，散射截面等於消散截面。圖 1。3 是一個小的無損耗負介電常數球的散射效率等值線圖，散射效率是介電常數（-3 到 -1）和尺寸引數的函式。圖中明亮的窄帶表示電多極子（electric multipoles）的強諧振區域。對於單個球體，諧振發生於

$\varepsilon = -1 - \dfrac{1}{n}, \quad n = 1,2,3,... \tag{1.8}$

其中

對應電偶極子（electric dipole），

對應電四極子（electric quadrupole），以此類推。不過對有限尺寸的散射球，這一關係並不確切。對於一個不導磁的散射球的電偶極子，考慮尺寸引數後其發生諧振的介電常數在數值上等於

$\varepsilon_{\rm{dipole}} = -2 - \dfrac{12}{5} · x^2\tag{1.9}$

其中尺寸引數為

$x = 2\pi a/ \lambda$

，是散射球半徑

與波長

$\lambda$

的函式。當

時，式（1。9）的誤差小於 1%。

對電四極子，類似的關係式為

$\varepsilon_{\rm{quadrupole}} = -\dfrac{3}{2}-\dfrac{5}{14}·x^2 \tag{1.10}$

值得注意的是，在

$\varepsilon=-2$

時，有一條近乎垂直的等高線（isocontour），覆蓋了

到

$x\simeq 0.5$

的區域，這意味著此時散射效率與散射體的尺寸無關。

1。3。1。2。 Accuracy of quasistatic prediction

既是式（1。3）的計算用到了全波（full-wave）洛倫茲-米方法，我們依然需要注意式（1。1）的極化率計算包括了尺寸遠小於波長的散射球的所有散射，吸收和消散行為。接下來我們需要驗證準靜態預測（quasistatic predictions）在真實的等離激元材料奈米粒子上的準確性，

常用的等離激元材料是銀，其在可見光頻段介電常數為負。其復介電常數可由實驗資料［23］擬合［22］為一個德魯德色散公式（Drude dispersion formula）

$\varepsilon_{\rm{Silver}}(\lambda) = \varepsilon$

其中

$\varepsilon_{\infty} = 5.5$

，

$\lambda_p = 130 {\rm{nm}}$

，

$\lambda_{d} = 30 {\rm{\mu m}}$

。在光波長

$320 {\rm{nm}} < \lambda < 700{\rm{nm}}$

的情形下該模型與實際吻合得很好。

圖1。4 極化率近似（準靜態，quasi-static prediction）與米氏全波求解（full Mie analysis）計算得到的散射效率的對比，藍實線為直徑 10nm 的銀奈米粒子，橘虛線為直徑 20nm 的銀奈米粒子。

圖1。5 與圖 1。4 類似的吸收效率的計算結果對比。

圖 1。4 與 1。5 展示了靜態分析的準確性。散射和吸收效率的漸近展開式給出了以下與極化率的聯絡

$Q_{\rm{sca}} \simeq \dfrac{8}{27}|\alpha|^2x^4, \quad Q_{\rm{abs}} \simeq = \dfrac{4}{3}\alpha$

其中

$\alpha$

是時極化率的虛部，表徵損耗。準靜態方法很好地定性解釋了兩種直徑下銀球的散射和吸收特性。唯一的缺點在於米氏求解中的輕微紅移（redshift）。注意到這種小尺寸散射體情形下吸收特性相較散射特性占主導地位。

1。3。1。3。 Non-spherical particles

雖然基於極化率的準靜態方法不能預測由於散射體尺寸造成的紅移，但意外的是，它可以很好地解釋散射體形狀和結構對等離激元特性峰值的影響。

要審視形狀對等離激元共振的影響，一個自然的思路是考慮橢球形的（ellipsoidal）奈米粒子。橢球形狀由

，

三個半軸引數決定。由此我們可以寫出

方向上的所謂去極化因子（depolarization factors ）

$N_x = \dfrac{a_xa_ya_z}{2}\int_0^{\infty}\dfrac{{\rm{d}}s }{(a + a_x^2)\sqrt{(s+a_x^2)(s+a_y^2)(s+a_z^2)}} \tag{1.13}$

另兩個方向的去極化因子可以類似寫出。三個計劃因子滿足以下關係

$N_x + N_y + N_z = 1 \tag{1.14}$

球體的去極化引數為

，圓盤為

，針形為

。

對一個各向同性介電常數為

$\varepsilon$

的橢球散射體，其極化向量（polarizability dyadic ）的三個分量為

$\alpha_i = \dfrac{\varepsilon - 1}{1 + N_i(\varepsilon - 1)} \quad (i = x,y,z) \tag{1.15}$

該式作為式（1。4）的一個推廣，揭示出局域等離激元共振（localized plasmon resonance）與奈米粒子的幾何尺寸密切相關。式（1。15）的奇點為

$\varepsilon_{\rm{1p}} = 1 - \dfrac{1}{N_i} \tag{1.16}$

介於 0 到 1 之間，因此只要形狀合適，奈米粒子在任何負的介電常數下都有可能發生共振。尤其是，當

從球形的 1/3 開始減小時，

$\varepsilon_{\rm{1p}}$

也隨之由 -2 開始減小，這意味著等離激元峰值的紅移。被拉長的物體往往有此效應。實際上，最有名的例子就是奈米棒（nanorods）［24］。

圖 1。6 中展示了兩種橢球形銀奈米粒子的的極化率分量。被研究的兩個特殊例子分別是長旋轉橢球（prolate spheroids，旋轉軸長於兩個橫半軸）扁平旋轉橢球（oblate spheroids，旋轉軸短於兩個橫半軸）。長旋轉橢球（針形橢球）中，旋轉軸方向激勵（axial excitation）的等離激元共振有明顯的紅移，橫向則有明顯的紅移；對扁平旋轉橢球，情況則相反。

圖1。6 長橢球（prolate spheroids）和扁橢球（oblate spheroids）極化率分量大小，軸比為 2：1：1 和 1：2：2 。實心藍線：沿旋轉軸極化率。橙色虛線：沿兩個橫軸極化率。介電常數見式（1。11）。

1。3。1。4。 Core–shell structures

另一種被廣泛研究的奈米粒子幾何結構是核殼結構（core–shell structure）。該結構有一個球體核心，外層被一個同心球殼包裹，但內外材料不同，其極化率遵循式（1。2）兩層粒子的情形。

圖1。7 互補的核殼複合散射球極化率分量大小。等離激元材料為銀，色散模型參見式（1。11）；介質為二氧化矽，可見光波段無色散介電常數為 2。25。銀佔總體積的比例為 g。藍色實線為 g = 0。9，橘色虛線為 g = 0。5，綠色虛線為 g = 0。3。

迷人的是等離激元核殼粒子會因核或殼是否是負介電常數而表現出不同的性質。如圖 1。7 所示，當一個等離激元核被一個介質殼（二氧化矽，介電常數 2。25）包裹時，極化率曲線在此出現紅移。紅移大小隨介質殼介電常數及相對厚度的增大而增大。

對於互補的情況（介質核被等離激元殼包裹），此時出現了兩個共振峰，這是因為現在金屬部分有兩個獨立的表面。有時這種在核殼結構中激發兩個共振的現象稱為模式雜化（mode hybridization）。這一現象已在中空金奈米粒子（hollow gold nanospheres）的實驗中被證實［25］。

1.3.2. Translation of dispersion results into mixtures

均質化會影響色散特性。複合材料會在有些頻率下出現強烈的響應特性，具體頻率是由組分引數，尤其是內含物（inclusions）決定的。

具體地說，假設有一種含有球形內含物的複合材料，如果內含物遵循德魯德色散模型

$\varepsilon(\omega) = \varepsilon_{\infty} - \dfrac{\omega_p^2}{\omega^2 - {\rm{j}} \omega \gamma } \tag{1.17}$

同時北京介質的介電常數為

$\varepsilon_d$

，如此複合材料應當遵循洛倫茲（Lorentzian）色散模型

$\varepsilon_{\rm{eff}} = \varepsilon_{\infty, \rm{eff}} + \dfrac{\omega^2_{p,\rm{eff}}}{\omega^2_{0,\rm{eff}} - \omega^2 + \rm{j}\omega \gamma_{eff}} \tag{1.18}$

其中有效高頻介電常數（effective high-frequency permittivity）為

$\varepsilon_{\infty,\rm{eff}} = \varepsilon_{d} + 3p\varepsilon_{d}\dfrac{\varepsilon_{\infty} - \varepsilon_d}{\varepsilon_{\infty} + 2\varepsilon_d - p(\varepsilon_{\infty} - \varepsilon_d)} \tag{1.19}$

有效等離子體頻率（effective plasma frequency）為

$\omega_{p,\rm{eff}} = \sqrt{p}\dfrac{3\varepsilon_d}{(1-p)\varepsilon_{\infty} + (2+p) \varepsilon_d} \omega_p \tag{1.20}$

有效諧振頻率（effective resonance frequency）為

$\omega_{0,\rm{eff}} = \sqrt{\dfrac{1-p}{(1-p)\varepsilon_{\infty} + (2+p)\varepsilon_d} } \omega_p \tag{1.21}$

有效阻尼振幅（effective damping amplitude）為

$\gamma_{\rm{eff}} = \gamma \tag{1.22}$

不過，關於複合材料中出現的物理效應的直觀理解，也可以從核殼粒子的有效介電常數與混合物的均質性之間的等效性中看出（參見 1。2 節）。這開啟了一個新的有趣的思考方向，即將奈米複合粒子的結論遷移到等離激元混合物領域。

圖1。8 銀與空氣混合物的有效介電常數（藍色實線為實部，橘色虛線為虛部）。銀的體積比例為 0。5，材料特性見式（1。11）。注意左右兩圖曲線的差異。（a）圖為空氣中分佈著銀球（葡萄乾布丁，raisin pudding），（b）圖為銀中分佈著空腔（瑞士乳酪，Swiss cheese）。

例如，圖 1。7 中互補核殼粒子光譜的定性差異意味著，被電介質包裹的銀球其特性會與球形空腔的瑞士乳酪型混合物（Swiss cheese type）有很大差別。圖 1。8 展示了銀與空氣體積各佔 0。5 時混合物的均質化模型特性。

由式（1。19）-（1。22），空氣中的銀粒子顯示出很強的洛倫茲共振（Lorentzian resonance），而互補的空穴結構則有著更平緩的色散特性。如果要實現低損耗和寬頻帶的一種

$\varepsilon = -1$

的複合材料，則瑞士乳酪（Swiss cheese）結構更為可取。在文獻［22］中，這一現象在寬頻帶亞波長透鏡的設計中得到了應用。

材料混合影響介電常數的頻率特性的另一個例子是弛豫型色散（relaxationtype dispersion）材料的均質化。具有永久偶極矩（permanent dipole moments）的物質，比如水，就會有這種特性，這通常稱為德拜色散（Debye dispersion）。

$\varepsilon(\omega) = \varepsilon + \dfrac{\varepsilon_s - \varepsilon_{\infty}}{1 + \rm{j}\omega \tau} \tag{1.23}$

其中

$\varepsilon_s$

與

$\varepsilon_{\infty}$

為低頻介電常數與高頻介電常數，

$\tau$

為弛豫週期（relaxation period）（

譯註：此處原文誤為弛豫頻率

）。在德拜媒質中，介電常數實部在弛豫頻率

$\omega_{\rm{rel}} = 1/\tau$

（relaxation frequency）處大小會劇減，對應著較高的損耗；不過虛部的峰值變化就沒有洛倫茲色散模型在共振時那麼劇烈。

當德拜媒質的粒子嵌入非色散的背景媒質中時，混合物的均質連續體（homogenized continuum）同樣遵循德拜色散模型，但是模型引數會發生改變。尤其是此時的弛豫頻率會變為

$\omega_{\rm{rel,eff}} = \omega_{\rm{rel}}\dfrac{(1-p)\varepsilon_s + (2+p) \varepsilon_e }{(1-p)\varepsilon_{\infty} + (2+p) \varepsilon_e} \tag{1.24}$

其中

$\varepsilon_e$

是背景媒質介電常數，

是德拜媒質材料所佔體積比。這種情形下頻率偏移會非常驚人，例如，水在室溫下

$\varepsilon_s \simeq 80.1$

，

$\varepsilon_{\infty} = 4.9$

，

$\tau \simeq 10.1 \rm{ps}$

，這意味著雲或雨的吸收峰會從

$16 \rm{GHz}$

偏移到

$200\rm{GHz}$

！圖 1。9 展示了這一物理效應。

圖1。9 水與空氣-水混合物的德拜色散特性，藍色實線為有效介電常數實部，橘色虛線為虛部。水的材料引數參見原文。（b）圖中水的體積佔比為 p = 0。1。

如果德拜媒質的內含物是橢球形，那麼弛豫偏移會更加明顯。對於在電場方向上有著去極化因子

，內含物介電常數為

$\varepsilon_{\rm{i}}$

、體積比為

的複合物，其有效介電常數分量為

$\varepsilon_{\rm{eff}} = \varepsilon_{\rm{e}} + p \varepsilon_{\rm{e}}\dfrac{\varepsilon_{\rm{i}} -\varepsilon_{\rm{e}} }{\varepsilon_{\rm{e}} + (1-p)N(\varepsilon_{\rm{i}} -\varepsilon_{\rm{e}} ) } \tag{1.25}$

對應的弛豫頻率為

$\omega_{\rm{rel,eff}} = \omega_{\rm{rel}}\dfrac{(1-p)N(\varepsilon_s - \varepsilon_e) + \varepsilon_e}{(1-p)N(\varepsilon_{\infty} - \varepsilon_e) + \varepsilon_e} \tag{1.26}$

但是，如果橢球內含物排列方向並不一致，則必須計算有效介電常數時必須考慮極化強度的方向。如果所有橢球都是隨機取向的，則沒有特殊的計劃方向，混合物是各向同性的，有效介電常數計算公式為

$\varepsilon_{\rm{eff}} = \varepsilon_{\rm{e}} + \varepsilon_{\rm{e}} \dfrac{\frac{p}{3}\Sigma_{j=x,y,z} \frac{\varepsilon_{\rm{i}} - \varepsilon_{\rm{e}} }{\varepsilon_{\rm{e}} +N_{j} (\varepsilon_{\rm{i}} -\varepsilon_{\rm{e}} ) } }{1 - \frac{p}{3} \Sigma_{j = x,y,z} \frac{N_j(\varepsilon_{\rm{i}} -\varepsilon_{\rm{e}} )}{\varepsilon_{\rm{e}} + N_{j} (\varepsilon_{\rm{i}} -\varepsilon_{\rm{e} }) } } \tag{1.27}$

最後，內部均質化與外部均質化原則之間是存在聯絡的，這使得上述弛豫偏移的結果可以被遷移到以德拜色散媒質為核、外部包裹電介質的複合材料上。

1.4. Homogenization is not simple arithmetic

前述章節強調了混合物的色散特性並揭示出其新奇的一面。除了均質化過程中隨頻率的變化外，混合過程中有效介電常數作為結構引數的函式也會表現出其他意想不到的特性。

計算混合物的宏觀質量密度只需計算各組分密度的比例平均值。但是宏觀介電常數卻不可如此即計算，它往往是各組分材料引數和幾何引數的非線性函式。有時候甚至可以構造有效介電常數高於任何組分介電常數的複合材料。這種現象在材料科學並不罕見，合金就具有優於其成分的效能。“整體大於部分的總和（whole being greater than the sum of its part）”，超材料正是如此。

1.4.1. Polarization limits

混合物的宏觀性質是可以預測的。當複合材料是由各向同性材料和無損耗材料組成，且各組分的介電係數（實部）很接近的時候，預測其性質就更加簡單。此時微觀結構的形態影響不大。然而，組分之間性質差距增大時，情況將發生改變。

任意的電介質混合物並沒有唯一的有效介電常數。當其中含有一定數量的內含物粒子時，即使所佔體積比相同，有效介電常數也會不同。但是材料引數數值總歸是有上下限的。通過蒙特卡洛模擬（Monte Carlo simulations），可以生成內含物隨機分佈的材料樣本。在不大可能的情況下，內含物會像平行平板一樣攢聚在連續介質中，此時材料將是各向異性的，兩個相互垂直的場激勵將得到兩個不同的響應

$\varepsilon_{\rm{eff,max}} = \dfrac{\varepsilon_{\rm{i}} \varepsilon_{\rm{e}} }{p\varepsilon_{\rm{e}} + (1-p)\varepsilon_{\rm{i}} }, \quad \varepsilon_{\rm{eff,min}} = p\varepsilon_{\rm{i}} + (1-p)\varepsilon_{\rm{e}} \tag{1.28}$

此即為所謂的維納邊界（Wiener bounds）［30］［31］，是由式（1。25）橢球混合規則中去極化因子分別取 1 和 0 得到的。

維納邊界給定的取值範圍仍比較寬泛，對此哈辛（Hashin）與希特里克曼（Shtrikman）給出了一個清晰的邊界（HS）［32］。實際上，HS 邊界的下限正對應式（1。4）的 MG 規則，而上限則是 MG 公式的互補，即內含物與背景媒質互換

$\varepsilon_{\rm{}HS,max} = \varepsilon_{\rm{eff,MG}}(\varepsilon_{\rm{i}}, \varepsilon_{\rm{e}}, p), \quad \varepsilon_{\rm{HS,min}} = \varepsilon_{\rm{eff,MG}}(\varepsilon_{\rm{e}}, \varepsilon_{\rm{i}}, 1-p) \tag{1.29}$

以上結論僅在內含物介電常數大於背景媒質（

$\varepsilon_{\rm{i}} > \varepsilon_{\rm{e}}$

）時有效。對於有空腔的“瑞士乳酪”情形（

$\varepsilon_{\rm{i}} < \varepsilon_{\rm{e}}$

），兩個邊界需要互換。

HS 邊界並不是最嚴格的。米爾頓（Milton）［33］，費爾德霍夫（Felderhof）［34］，海辛（Helsing）［35］都提出過更嚴格的限制。

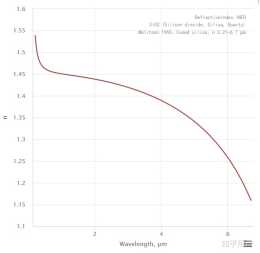
接下來將維納邊界與 HS 邊界應用到對雪的研究。乾燥的雪是空氣基質中冰粒（微波波段介電常數為 3。19）的混合物。測量資料［36］、維納邊界函式、HS 邊界函式的曲線如圖 1。10 所示。

圖1。10 冰與空氣混合物（幹雪）的物質特性上下界，有效介電常數被表示為雪密度 ρ 的函式。冰的體積比為 p = ρ / ρ_ice，其中冰的密度 ρ_ice = 0。917 g/cm^3。冰的介電常數為 3。19。圖中的紅色散點即為實際測量資料。

圖 1。10 中雪的介電常數變化規律是隨密度而單調遞增的。但是，如果介質響應變得更為複雜，材料的特性也就更像超材料了，如此材料引數也許會超出理論極限。這在強損耗與交叉耦合的情形下更為常見，比如磁電耦合響應（magnetoelectric response）。

圖 1。11 說明組分材料中損耗增加可能會使混合物有效介電常數增大。曲線顯示了明顯的極化增強效應，換句話說，當損耗足夠大的時候，有效介電常數

$\varepsilon$

的實部可能會遠大於任意組分的實部。即便是用其他的混合物特性公式分析，極化增幅可能會不同，但定性結果仍是不變的［28］。圖 1。11（b）還給出了 HS 邊界（MG 公式及其互補情形），在

$\varepsilon_{\rm{eff}}$

複平面上邊界之間的可取值範圍相當寬泛，其他的混合物公式的結果也都落在這個區域中。

圖1。11 （a） MG 理論下不同內含物損耗對應的有效介電常數實部大小：藍色實線 ε_i = 2 - j0，橘色虛線 ε_i = 2 - j5，綠色虛線 ε_i = 2 - j10。環境媒質為空氣，ε_e = 1。（b） HS 模型在 ε_eff 複平面上的上下限。

值得注意的是圖 1。11 中的極化率增強效應並不只是個理論預測，而是已在許多領域中得到驗證，如膠體和生物細胞懸浮液（colloidal and biological cell-suspensions）［38］。這一現象與隔開電解質溶液（electrolyte solutions）的細胞膜（membranes）有關，被稱為麥克斯韋-瓦格納效應（Maxwell-Wagner effect）［39］，在生物電磁學（bioelectromagnetics）中也被稱為阿爾法色散（alpha dispersion），主要發生在低頻段（10 赫茲到數千赫茲）。

1.4.2. Percolation behavior

對於各組分材料引數相差甚遠的混合物，必須要考慮滲濾（percolation）［40］效應的存在，即微觀結構的極小改變對混合物宏觀性質的巨大影響。這意味著組分材料所佔體積比例與混合物有效介電常數之間的函式關係是非線性的。

圖1。12 布呂熱曼模型在有損情形下對有效介電常數實部的預測。藍色實線 ε_i = 10 - j0，橘色虛線 ε_i = 10 - j100，綠色虛線 ε_i = 210- j200：損耗是逐漸增大的。環境媒質為空氣，ε_e = 1

對於高損耗的混合物，滲濾效應是明顯的。圖 1。12 展示了布呂熱曼模型對複合材料有效折射率的預測，研究物件是有損耗的球形內含物嵌入的自由空間。此時宏觀的介電常數曲線變化不再平滑，當內含物損耗增加時曲線幾乎是不連續的。虛部

$\varepsilon_{\rm{eff}}$

幾乎是 0，直到

大於所謂的滲濾閾值（percolation threshold），大約在 1/3 左右，此後虛部逐漸增大直到與實部相近。介電常數實部曲線則在閾值處經歷了一個峰值變化，急劇衰減後繼續隨著體積分數

的增加而增大。

值得注意的是，運用不同的理論模型研究滲濾行為得到的結果可能是不同的，儘管物理現象本身並沒有變。由式（1。7）出發，假設內含物介電常數相對背景媒質非常大，如此該式可簡化為

$\varepsilon_{\rm{eff}} = \varepsilon_{\rm{e}}\dfrac{1+p(2-\nu)}{1- p (1+\nu)} \tag{1.30}$

該式在

$p = 1/(1+\nu)$

處有奇點。該值可被理解為滲濾閾值。在

$\nu = 2$

的布呂熱曼模型下，該式與圖 1。12 的例子對應。有序晶格（ordered lattices）情形下更接近 MG 理論模型，而布呂熱曼模型則因其對稱性而被廣泛應用於隨機結構的複合物。對於

$\nu = 0$

的 MG 模型，其滲濾閾值在

。

1.4.3. Magnetoelectric coupling

磁電耦合（magnetoelectric coupling）是一個有趣的材料電磁響應問題，電激勵會產生磁響應，反之亦然。如果這種媒質是各向同性的（響應與激發場向量的方向無關），對應的就是雙各向同性材料（bi-isotropic materials）［41］。雙各向同性的本構關係可以用涵蓋電磁場量

$(\bm{\rm{E,H}})$

與電磁通量密度

$(\bm{\rm{D,B}})$

關係的矩陣來表示：

$\binom{\bm{\rm{D}}/\sqrt{\varepsilon_0}}{\bm{\rm{B}}/\sqrt{\mu_0}} = \begin{pmatrix} \varepsilon & \chi - {\rm{j}} \kappa \\ \chi + {\rm{j}} \kappa & \mu \end{pmatrix} \binom{\sqrt{\varepsilon_0} \ \bm{\rm{E}} }{\sqrt{\mu_0} \ \bm{\rm{B}}} = \mathcal{M} \binom{\sqrt{\varepsilon_0} \ \bm{\rm{E}} }{\sqrt{\mu_0} \ \bm{\rm{B}}} \tag{1.31}$

式中場量與通量均以自由空間介電常數和磁導率

$(\varepsilon_0, \mu_0)$

進行標準化，因此單位相同（能量密度的平方根

$\sqrt{{\rm{Ws}}/m^3}$

），矩陣

$\mathcal{M}$

也是無量綱的（dimensionless）。電磁交叉耦合是由手性引數

$\kappa$

（chirality parameter）與非互易引數

$\chi$

（non-reciprocity parameter）。手性引數在研究手性媒質（handed media）時會用到，

$\kappa$

也稱為巴斯德引數（Pasteur parameter）［41］；非互易引數

$\chi$

則被稱為特勒根引數（Tellegen parameter）［42］。

對於包含雙各向同性媒質的混合物，其有效介電常數可直接由式（1。4）出發，以磁電耦合引數矩陣替代非耦合情形下的介電常數得到。例如，雙各向同性的 MG 公式的可寫為

$\mathcal{M}_{\rm{eff}} = \mathcal{M}_{\rm{e}} + 3p \mathcal{M}_{\rm{e}} · [ \mathcal{M}_{\rm{i}} + 2 \mathcal{M}_{\rm{e}} - p( \mathcal{M}_{\rm{i}} - \mathcal{M}_{\rm{e}} )^{-1} ] · ( \mathcal{M}_{\rm{i}} - \mathcal{M}_{\rm{e}}) \tag{1.32}$

其中

$\mathcal{M}_{\rm{e}}$

為環境媒質的引數矩陣，

$\mathcal{M}_{\rm{i}}$

為內含物媒質的引數矩陣，

是內含物所佔體積比。

考慮一個兩種手性材料的混合物，兩種組分材料結構相同，但互為映象。這意味著它們具有相同的介電常數和磁導率（

$\varepsilon_i = \varepsilon_e$

，

$\mu_i = \mu_e$

），但是手性引數符號相反

$\kappa_i = -\kappa_e$

。

圖1。13 手性材料混合物在 MG 理論下的有效介電常數曲線，其中一種材料的結構是另一種材料的映象。兩種材料的引數取值為 ε_i = ε_e = 2，μ_i = μ_e = 2，κ_i = -κ_e = 1。

圖 1。13 展示了

$\varepsilon_i = \varepsilon_e = \mu_i = \mu_e = 2$

，

$\kappa_i = -\kappa_e = 1$

情形下混合物的有效介電常數變化曲線與有效手性引數變化曲線。可以看出，即使兩種材料具有相同的介電常數，混合物的有效介電常數也低於各組分的有效介電常數（有效磁導率也是如此）。此外，手性引數從環境材料的取值到內含物材料的取值單調變化，但變化規律並不對稱：對於 p = 0。5 的混合物，手性雖然很弱，但並沒有完全消失。

1.4.4. Hyperbolic media and anomalous losses

各向異性（anisotropy）是材料複雜電磁響應研究的一個很有趣方向，特別是當各向異性與等離激元聯絡起來時，所產生的材料效應會格外有趣。

1。4。4。1。 Cartesian and spherical uniaxial anisotropy

微觀結構的排列方式導致了宏觀媒質響應的各向異性，如此介電常數必須以更多的引數表徵，而非一個標量。各向異性最簡單的表達方式是單軸的（uniaxial）。對於單軸介質，介電常數張量有兩個分量：軸向（axial）分量（

$\varepsilon_r$

）與橫向（transversal）分量（

$\varepsilon_t$

）。圖 1。14 展示了兩個可用這種方式描述宏觀行為的複合結構，其中，堆疊平板（stacked-plates）結構的軸向為板面法向，圓柱陣列（aligned-needles）結構的軸向與圓柱單元軸向一致。

圖1。14 單軸兩相（Uniaxial two-phase）複合結構：堆疊平板與圓柱陣列。

圖1。14 球層型（洋蔥狀）與放射型（徑向刺狀）混合球體是等效 RA。

與圖 1。14 的笛卡爾座標系下的情形不同，單軸各向異性也可以是徑向（radial）與球對稱（spherically symmetric）的。圖 1。15 就描繪了這樣一個情形，其中顯示了被稱為 RA 球體的內含物。RA 球結構的兩種型別為球層型（bulbic sphere；洋蔥狀分層，onion-like layers）和放射型（porcupic sphere；豪豬刺，porcupine spikes）［44］。更進一步，如果允許橫向各向異性在兩個互相垂直的方向（如經度和緯度）上介電常數分量不同，如此便能得到更一般的球各向異性情形，這一情形也被稱為系統異性（systropic）。

如果均質化能保證在亞波長條件下進行，那麼球層型和放射型單軸結構的均質化就很簡單了：所有的四個分量都是式（1。25）同向排列橢球內含物混合公式的特殊情形。對於堆疊平板結構或球層結構，軸向介電常數對應於去極化因子

，橫向介電常數對應

；對於圓柱陣列或放射結構，軸向分量對應

，橫向分量對應

。

和

的情況分別給出了維納邊界的上下界，對應式（1。28）。這意味著，對於球層結構，軸向介電常數小於橫向介電常數（

$\varepsilon_r < \varepsilon_t$

；負單軸性，negative uniaxiality）；反之，對於放射結構，軸向介電常數大於橫向介電常數（

$\varepsilon_r > \varepsilon_t$

；正單軸性，positive uniaxiality）。

圖1。16 具有單軸各向異性結構的銀矽複合材料。兩種組分體積分數相等。藍實線：介電常數實部軸向分量。橙虛線：介電常數實部橫向分量。銀的模型見式（1。11），二氧化矽的介電常數設為 2。25。

然而，當球層結構或放射結構中的任一組分為等離激元時，軸向和橫向的有效介電常數分量也可能發生變化。當介電常數張量特徵值異號時，媒質被稱為不定媒質（indefinite）或雙曲（hyperbolic）媒質。圖 1。16 展示了這種效應，其中銀-矽複合材料（體積分數各為 50%）的介電常數張量實部各分量被表示為波長的函式。可以看出在兩種結構中，都出現了寬頻雙曲行為（broadband hyperbolic behavior）。不同之處在於，球層結構的橫向介電常數為負，放射結構的軸向介電常數為負。

1。4。4。2。 Radially anisotropic sphere

RA 球體的有趣性質已被廣泛研究［47，48］，其在隱身與反常吸收截面（anomalous absorption cross-section）上具有很大的潛力，而且這些性質均可以用準靜態的方法加以研究。

RA 球體的內部結構是複雜的，不均勻的（介電常數張量本徵值不是常數）和各向異性的，但從外部看，它是完全球對稱的，等價的宏觀特性也是各向同性的。因此，它的極化率是一個標量。

根據準靜態分析，RA 球的極化率可寫為

$\alpha_{\rm{RA}} = 3 \dfrac{\varepsilon_r \sqrt{1+8\varepsilon_t/\varepsilon_r} - \varepsilon_r - 2}{ \varepsilon_r\sqrt{1+8\varepsilon_t/\varepsilon_r} - \varepsilon_r + 4 } \tag{1.33}$

當

$\varepsilon_r = \varepsilon_t$

時，上式退化為式（1。1）的情形。當

$\varepsilon_r \neq \varepsilon_t$

時，我們可以得到一些有趣的性質。

首先，當

$\varepsilon_t = \dfrac{\varepsilon_r + 1}{2\varepsilon_r}, \quad \varepsilon_r > 0 \quad {\rm{or}} \quad \varepsilon_r < -2 \tag{1.34}$

時，極化率衰減為 0。這意味著在靜電場下，球體是不可見的。當兩材料介電常數均為正數時，這一現象有一個直觀的解釋：兩個引數

$\varepsilon_r$

與

$\varepsilon_t$

的組合，一個小於 1，一個大於 1，兩者可以相互抵消對方的物理效應，使得球體對外隱形。內部均質球的有效介電常數

$\varepsilon_{\rm{eff}} = 1$

。不太明顯的一點是，在

$\varepsilon_r$

為負但

$\varepsilon_t$

為正的區域，極化率也會衰減為 0（非確定各向異性的區域，indefinite anisotropy）。在這種情況下，即使球體不會對外部場造成任何擾動，散射體的中心仍會有一個場強峰值，。

另一方面，

$\alpha_{\rm{RA}}$

的奇點處對應一個等離激元偶極子共振峰。有趣的是有兩種型別的奇點。奇點滿足的條件是

$\varepsilon_t = \dfrac{2-\varepsilon_r}{\varepsilon_r}, \quad \varepsilon_r < 0 \quad {\rm{or}} \quad \varepsilon_r > +4 \tag{1.35}$

第一種共振奇點是各向同性情形下靜電共振點

$\varepsilon = -2$

的推廣，並對應式（1。35）中的

$\varepsilon_r < 0$

，即完全等離激元（雙負，double-negative）區域。奇點的另一分支出現在

$\varepsilon_r > 0$

，

$\varepsilon_t < 0$

的不定象限（indefinite quadrant）。這兩種情形下的場分佈是不同的：第一種情形是普通的區域性表面等離激元，而對於第二種不確定區域奇點，場的能量集中在 RA 等效球的中心。

圖1。17 RA 球在 ε_r - ε_t 平面上的極化特性。藍色實線是隱身輪廓線，橙色虛線標記出奇點條件。淡綠色陰影區為異常吸收區。

最值得關注的是區域

$\varepsilon_t / \varepsilon_r < -1/8$

，此時式（1。33）的平方根表示式就複雜了。換句話說，RA 球將包含一個虛部，即使它的介電常數分量是實數。這種現象被稱為反常吸收（anomalous absorption），文獻［48］對此作了詳細的研究。分析需要對球中心的場行為進行正則化（regularization），並推出 RA 球的聚焦效應使其能夠以任意程度增強固有損耗（intrinsic losses）的影響。圖 1。17 繪製了

$\varepsilon_r - \varepsilon_t$

複平面上的各個 RA 區域。

RA 球的異常吸收現象也可以在動態激勵（dynamic excitation）下加以研究。圖 1。18 展示了尺寸引數

的 RA 球的吸收效率，比較了準靜態分析的預測結果（由式（1。33）的虛部結合式（1。12）計算得到）與全波Mie散射計算結果。即使現在的球並不能滿足亞波長條件，也可以看出靜態分析很好地解釋了散射截面特性，而且在

$-8 < \varepsilon_r/\varepsilon_t < 0$

區域的異常吸收也得到了很好的解釋。然而，動態分析也揭示了額外的異常吸收，儘管在量級上很小。與圖 1。17 中淺綠色區域相比，雙曲各向異性中這一現象的發生更多位於負的

$\varepsilon_r$

區域。

圖1。18 尺寸引數 x = 0。5 的 RA 球的吸收（藍色實線）和散射（橙色虛線）效率。切向的介電常數分量為 ε_t = 1，而徑向的介電常數分量 ε_r 是變化的。左右兩圖比較了準靜態分析和全波各向異性 Mie 分析的結果。

1。5。 Conclusions： Metamaterials as Vessels of Emergence

對超材料的研究需要將微觀結構轉換成宏觀影象。宏觀尺度上新特性會出現，但代價是犧牲微觀結構的資訊，不過這是值得的。超材料將是更多新興技術發展的溫床。

本章的重點是用經典的混合理論來研究超材料的性質，重點在於均質化如何能在複合材料中產生新的特性。混合物由普通材料組成，其性質遵循已知的模型，如德魯德模型或德拜模型。然而，即使是將組分以簡單的結構引數組合，結果也會呈現出與原始材料完全不同的特性。這是一個類似於元胞自動機（cellular automata）［49］的新世界，一個簡單的規則可以產生非常複雜的行為，而且不能從初始條件直接預測，只能一步步地推導最終結果，沒有捷徑可走。

超材料研究領域是什麼？定義非常寬泛，有時可能包括那些作為超材料激發結構的元件，如形狀類似於開口環（split-ring）的天線。撇開這些不談，主流的超材料定義就是一個宏觀的連續體，其中的微觀結構產生了集體效應。均質化是超材料研究的核心，這要求內含物的結構在空間尺度上遠小於波長。這也正是混合原理的領域，主要基於準靜態分析和廣義拉普拉斯方程（generalized Laplace equation）。在本章中，從微波到光學的許多例子都證明了混合規則在描述有效介電常數上是有效的。

電磁均質化有著悠久的歷史。正如克里斯蒂安·布羅索（Christian Brosseau）［50，51］所指出的那樣，它的發展可看作一出五幕劇。20 世紀頭十年，MG 理論的興起啟發了 20 世紀 30 年代的布呂熱曼有效介質均勻化；哈辛、希特克里曼等在 20 世紀 60 年代提出的邊界原理擴充套件了對滲濾行為的理解。最後，計算機技術的發展徹底改變了計算電磁學，為模擬隨機混合和測試有效介質理論帶來了前所未有的可能性。

Reference

1。 Sihvola， A。（2003）。 Electromagnetic emergence in metamaterials。 In eds。 S。 Zouhdi， A。 Sihvola， and M。 Arsalane， Advances in Electromagnetics of Complex Media and Metamaterials， vol。 89， pp。 1–17 （Kluwer Academic Publishers， Dordrecht）。

2。 Sihvola， A。（2007）。 Metamaterials in electromagnetics， Metamaterials 1（1）， pp。 2–11。

3。 Sihvola， A。（2009）。 Metamaterials： A personal view， Radioengineering 18（2： Part I： Special Issue on Artificial EM Materials and Metamaterials）， pp。 90–94。

4。

https：//

en。wikipedia。org/wiki/M

etamaterial

，（accessed 27 August 2015）。

5。 Walser， R。 M。（2000）。 Metamaterials： What Are They？ What Are They Good For？ Talk at American Physical Society Meeting， Minneapolis， pp。 20–24。

6。 Walser， R。 M。（2003）。 Electromagnetic metamaterials。 In eds。 A。 Lakhtakia， W。 S。 Weiglhofer， and I。 J。 Hodgkinson， Complex Mediums II： Beyond Linear Isotropic Dielectrics， vol。 4467， pp。 1–15。 SPIE。

7。 Engheta， N。（2008）。 Metactronics： Optical circuits and information processing in nanoworld。 In Proc。 of META’08， NATO Advanced Research Workshop， p。 533。

8。 Lakhtakia， A。（2015）。 From bioinspired multifunctionality to mimumes， Bioinspir。 Biomim。 Nan。 4， pp。 168–173。

9。 Shamonina， E。 and Solymar， L。（2007）。 Metamaterials： How the subject started， Metamaterials 1（1）， pp。 12–18。

10。 Sihvola， A。（1999）。 Electromagnetic Mixing Formulas and Applications。 vol。 47， Electromagnetic Waves Series，（IEE Publishing， London）。

11。 Milton， G。 W。（2002）。 The Theory of Composites。（Cambridge University Press， Cambridge）。

12。 Chettiar， U。 K。 and Engheta， N。（2012）。 Internal homogenization： Effective permittivity of a coated sphere， Opt。 Exp。 20（21）， pp。 22976–22986。

13。 Sihvola， A。， Kettunen， H。 and Wall´en， H。（2013）。 Mixtures and composite particles： Correspondence of effective description。 In Proc。 EMTS 2013， URSI International Symposium on Electromagnetic Theory， pp。 908–911， pp。 21–24 May， Hiroshima， Japan。

14。 Garnett， J。 C。 M。（1904）。 Colours in metal glasses and metal films， Trans。 R。 Soc。 203， pp。 385–420。

15。 Bruggeman， D。 A。 G。（1935）。 Berechnung verschiedener physikalischer Konstanten von heterogenen Substanzen。 I。 Dielektrizit¨atskonstanten und Leitf¨ahigkeiten der Mischk¨orper aus isotropen Substanzen， Ann。 Phys。 24， pp。 636–679。

16。 Sihvola， A。（1989）。 Self-consistency aspects of dielectric mixing theories， IEEE Trans。 Geosci。 Remote Sens。 27（4）， pp。 403–415。

17。 Elliott， R。 J。， Krumhansl， J。 A。 and Leath， P。 L。（1974）。 The theory and properties of randomly disordered crystals and related physical systems， Rev。 Mod。 Phys。 46， pp。 465–543。

18。 Bohren， C。 F。 and Huffman， D。 R。（1983）。 Absorption and Scattering of Light by Small Particles （Wiley， New York）。

19。 Lorenz， L。（1890）。 Lysbevægelser i og uden for en af plane Lysbølger belyst Kugle， Kongelige Danske Videnskabernes Selskabs Skrifter。 6， pp。 2–62。

20。 Mie， G。（1908）。 Beitr¨age zur Optik tr¨ uber Medien， speziell kolloidaler Metall¨osungen， Ann。 Phys。 25， pp。 377–445。

21。 Strutt， J。 W。（1871）。 On the light from the sky， its polarization and colour， Philosophical Magazine 41， pp。 107–120， pp。 274–279。

22。 Wall´en， H。， Kettunen， H。 and Sihvola， A。（2009）。 Composite near-field superlens design using mixing formulas and simulations， Metamaterials 3（3–4）， pp。 129–139。 23。 Johnson， P。 B。 and Christy， R。 W。（1972）。 Optical constants of the noble metals， Phys。 Rev。 B。 6， pp。 4370–4379。

24。 Smythe， E。 J。， Cubukcu， E。 and Capasso， F。（2007）。 Optical properties of surface plasmon resonances of coupled metallic nanorods， Opt。 Exp。 15（12）， pp。 7439–7447。

25。 Sadecka， K。， Toudert， J。， Surma， H。 B。 and Pawlak， D。 A。（2015）。 Temperature and atmosphere tunability of the nanoplasmonic resonance of a volumetric eutectic-based Bi2O3-Ag metamaterials， Opt。 Exp。 23（15）， p。 241792。

26。 Sonnefraud， Y。， Verellen， N。， Sobhani， H。， Vandenbosch， G。 A。， Moshchalkov， V。 V。 Dorpe， P。 V。， Nordlander， P。 and Maier， S。 A。（2010）。 Experimental realization of subradiant， superradiant， and Fano resonances in ring/disk plasmonic nanocavities， ACS Nano 4（3）， pp。 1664–1670。

27。 Schwartzberg， A。 M。， Olson， T。 Y。， Talley， C。 E。 and Zhang， J。 Z。（2006）。 Synthesis， characterization， and tunable optical properties of hollow gold nanospheres， J。 Phys。 Chem。 B 110（40）， pp。 19935–19944。

28。 Sihvola， A。（2002）。 How strict are theoretical bounds for dielectric properties of mixtures？， IEEE Trans。 Geosci。 Remote Sens。 40（4）， pp。 880–886。

29。 Pawlak， D。 A。， Turczynski， S。， Gajc， M。， Kolodziejak， K。， Diduszko， R。， Rozniatowski， K。， Smalc， J。 and Vendik， I。（2010）。 Metamaterials： How far are we from making metamaterials by self-organization？ The microstructure of highly anisotropic particles with an SRR-like geometry， Adv。 Funct。 Mater。

20（7）， pp。 1116–1124。 30。 Wiener， O。（1904）。 Lamellare doppelbrechung， Physikalische Zeitschrift 5（12）， pp。 332–338。

31。 Wiener， O。（1910）。 Zur theorie der refraktionskonstanten， Berichte Uber die ¨ Verhandlungen der K¨oniglich-S¨achsischen Gesellschaft der Wissenshaften zu Leipzig （62）， pp。 256–277。

32。 Hashin， Z。 and Shtrikman， S。（1962）。 A variational approach to the theory of the effective magnetic permeability of multiphase materials， J。 Appl。 Phys。 33（10）， pp。 3125–3131。

33。 Milton， G。 W。（1981）。 Bounds on the complex permittivity of a two component composite material， J。 Appl。 Phys。 52（8）， pp。 5286–5293。

34。 Felderhof， B。（1984）。 Bounds for the complex dielectric constant of a twophase composite， Phys。 A。 126（3）， pp。 430–442。

35。 Helsing， J。（1993）。 Bounds to the conductivity of some two-component composites， J。 Appl。 Phys。 73（3）， pp。 1240–1245。

36。 M¨atzler， C。（1996）。 Microwave permittivity of dry snow， IEEE Trans。 Geosci。 Remote Sens。 34， pp。 573–581。

37。 Callen， H。 B。（1960）。 Thermodynamics。（John Wiley & Sons， New York）。

38。 Schwan， H。 P。， Schwarz， G。， Maczuk， J。 and Pauly， H。（1962）。 On the lowfrequency dielectric dispersion of colloidal particles in electrolyte solution， J。 Phys。 Chem。 66（12）， pp。 2626–2635。

39。 Wagner， K。 W。（1914）。 Erkl¨arung der dielektrischen Nachwirkungsvorg¨ ange auf Grund Maxwellscher Vorstellungen， Archiv f¨ ur Elektrotechnik 2（9）， pp。 371–387。

40。 Stauffer， D。 and Aharony， A。（1994）。 Introduction to Percolation Theory。（Taylor & Francis， London， U。K。）。

41。 Lindell， I。 V。， Sihvola， A。 H。， Tretyakov， S。 A。 and Viitanen， A。 J。（1994）。 Electromagnetic Waves in Chiral and Bi-Isotropic Media （Artech House， Norwood， Massachusetts）。

42。 Tellegen， B。 D。 H。（1948）。 The gyrator， a new electric network element， Philips Res。 Rep。 3（2）， pp。 81–101。

43。 Sihvola， A。 H。（1992）。 Bi-isotropic mixtures， IEEE Trans。 Antennas Propag。 40（2）， 188–197。

44。 Rimpil¨ainen， T。， Wall´en， H。 and Sihvola， A。（2015）。 Radial anisotropy in spheroidal scatterers， IEEE Trans。 Antennas Propag。 63（7）， pp。 3127–3135。

45。 Rimpil¨ainen， T。， Pitkonen， M。， Wall´en， H。， Kettunen， H。 and Sihvola， A。（2014）。 General systropy in spherical scatterers， IEEE Trans。 Antennas Propag。 62（1）， pp。 327–333。

46。 Poddubny， A。， Iorsh， I。， Belov， P。 and Kivshar， Y。（2013）。 Hyperbolic metamaterials， Nat。 Photon。 7（12）， pp。 948–957。

47。 Kettunen， H。， Wall´en， H。 and Sihvola， A。（2013）。 Cloaking and magnifying using radial anisotropy， J。 Appl。 Phys。 114（4）， p。 044110。

48。 Wall´en， H。， Kettunen， H。 and Sihvola， A。（2015）。 Anomalous absorption， plasmonic resonances， and invisibility of radially anisotropic spheres， Radio Science 50（1）， pp。 18–28。

49。 Wolfram， S。（2002）。 A New Kind of Science。（Wolfram Media， Champaign， Illinois）。

50。 Brosseau， C。（2006）。 Modelling and simulation of dielectric heterostructures： A physical survey from an historical perspective， J。 Phys。 D： Appl。 Phys。 39， pp。 1277–1294。

51。 Sihvola， A。（2013）。 Homogenization principles and effect of mixing on dielectric behavior， Photon。 Nanostruct。 11（4）， pp。 364–373。

標簽：介電常數 PP 材料極化引數

上一篇:別再對分類變數進行獨熱編碼！你還有更好的選擇

下一篇：視鏡連線的幾種方式