什麼是齊次座標系?為什麼要用齊次座標系？

機器人基礎數學知識-什麼是

齊次座標系

？為什麼要用齊次座標系？

這篇文章內容主要學習自參考連結［1］［2］中的內容。如有侵權，請聯絡刪除~~

在瞭解齊次座標與非齊次座標之前，首先了解一下

笛卡爾座標系

。

一、笛卡爾座標系

笛卡爾座標系

笛卡爾座標系（Cartesian coordinates）就是直角座標系和

斜角座標系

的統稱。

相交於原點的兩條數軸，構成了平面仿射座標系。 如兩條數軸上的度量單位相等，則稱此仿射座標系為笛卡爾座標系。

兩條數軸互相垂直的笛卡爾座標系，稱為笛卡爾直角座標系，否則稱為笛卡爾斜角座標系。

笛卡爾直角座標系

就是我們常見的直角座標系，包括平面直角座標系、

空間直角座標系

。

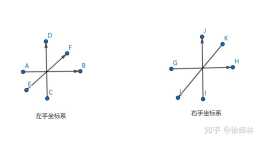
也就是下圖中的關係：

二、什麼是齊次（Homogeneous）座標系？為什麼要用齊次座標系？

這部分內容主要翻譯自

http：//www。

songho。ca/math/homogene

ous/homogeneous。html

1。 問題： 兩條平行線能相交

在歐氏（幾何）空間，同一平面的兩條平行線永遠不能相交，這是我們都熟悉的一種場景。 然而，在透視空間裡面，兩條平行線可以相交，例如：火車軌道隨著我們的視線越來越窄，最後兩條平行線在無窮遠處交於一點。

歐氏空間

（或者笛卡爾空間）描述2D/3D幾何非常適合，但是這種方法卻不適合處理透視空間的問題（實際上，

歐氏幾何

是透視幾何的一個子集合），2D笛卡爾座標可以表示為

。

如果一個點在無窮遠處，這個點的座標將會

，在歐氏空間中，這就變得沒有意義。平行線在透視空間的無窮遠處交於一點，但是在歐氏空間卻不能表示，數學家發現了一種方式來解決這個問題 （那就是 齊次座標）。

2。 解決方法：齊次座標

齊次座標是由 August Ferdinand Möbius 引入的，使其在投影空間中進行圖形和幾何計算成為可能。

簡而言之，齊次座標就是用N+1維來代表N維座標

我們可以在一個2D笛卡爾座標末尾加上一個額外的變數w來形成 2D齊次座標。因此，一個在笛卡爾座標系下的點$（X， Y）$在齊次座標裡面變成了

，並且有

例如，笛卡爾座標系下

齊次座標可以表示為

，如果點

移動到無限遠處，在笛卡爾座標下它變為

，然後它的齊次座標表示為

，因為

。 注意這樣的話，我們可以不用 ”

“ 來表示一個無窮遠處的點了~~~

3。 為什麼叫齊次座標？

如前面所述，我們

把齊次座標轉化為笛卡爾座標的方法是前面n-1個座標分量分別除以最後一個分量即可

。

把座標從齊次座標轉換為笛卡爾座標，我們可以發現這樣一個事實。看下面的例子：

你會發現

，

和

對應同一個歐幾里得點（笛卡爾空間點）

。任何標量的乘積，

對應 笛卡爾空間裡面的都是

。因此，這些點是“齊次的 （Homogeneous adj。 同類的，同質的）”，因為他們代表了歐氏空間（

笛卡爾座標空間

）裡面的同一個點。換句話說，齊次座標有規模不變性。

4。 證明：兩條直線可以相交

考慮如下歐幾里得空間的

線性系統方程

：

我們知道在笛卡爾座標系裡面，如果

該方程組無解。如果

，兩條直線就相同了。

在透視空間裡中，讓我們用齊次座標 $x/w， y/w$ 分別代替 $x ，y$ 重寫這個方程：

可以化為：

現在我們有一個解

，因為

，所以

。因此，兩條直線相交於

，這個點在無窮遠處。

齊次座標是計算機圖形學中非常有用的基礎概念，比如將3D場景投影到2D平面上。

三、總結

齊次座標的意義：

如果一個點在無窮遠處，這個點的座標將會

，在歐氏空間中，這就變得沒有意義。如果使用齊次座標，平行線在透視空間的無窮遠處交於一點，這樣就實現了對於無窮點的表示，但是在歐氏空間不能表示無窮點。

也就是說

透過利用齊次座標就可以表示無窮遠處的點。

例如： 笛卡爾座標系下

齊次座標可以表示為

，如果點

移動到無限遠處，在笛卡爾座標下它變為

，然後它的齊次座標表示為

，因為

。 注意這樣的話，我們可以不用 ”

” 來表示一個無窮遠處的點了~~~

四、參考文獻

［1］ 百度百科。 笛卡爾座標系 ［EB/OL］。 （2021-01-12） ［2021-05-20］。

https：//

baike。baidu。com/item/

笛卡爾座標系/4522878？fr=aladdin

［2］ Song Ho Ahn。 Homogeneous Coordinates ［EB/OL］。 （2016） ［2021-05-20］。

http：//www。

songho。ca/math/homogene

ous/homogeneous。html

［3］ （參考連結［2］的翻譯） JANESTAR。 關於齊次座標的理解（經典） ［EB/OL］。 （2015-03-13） ［2021-05-20］。

https：//

blog。csdn。net/janestar/

article/details/44244849